2025年非线性泛函分析及其应用学术研讨会

（2025年10月31日-11月2日）

报告摘要

Multiple solutions for nonhomogeneous Klein-Gordon-Maxwell system with Berestycki-Lions conditions

吴行平  西南大学

报告摘要：This paper is concerned with a kind of nonhomogeneous Klein–Gordon–Maxwell system− Δ u−(2 ω+ ϕ) ϕ u= g (u)+ h (x), in R 3, Δ ϕ=(ω+ ϕ) u 2, in R 3, where ω> 0 is a constant and g satisfies the Berestycki–Lions type conditions. By using Ekelands variational principle, the mountain pass theorem, Pohožaev identity and some new tricks, two nontrivial solutions can be obtained here

报告人简介：西南大学教授，硕导，美国《数学评论》评论员。曾获重庆市人民政府自然科学二等奖,和三等奖。1982年9月至1986年7月于西南师范大学数学系读本科;1986年8月至1989年6月于西南师范大学数学系读研究生;1989年6月获硕士学位。1989年7月留校工作; 1992年晋升为讲师; 1998年6月晋升为副教授; 2004年晋升为教授。主要研究领域是非线性泛函分析、非线性椭圆方程、二阶Hamilton系统。发表论文多篇。

Li-Lin公开问题及相关研究

唐之韵 博士后（西南大学）

报告摘要： 2012年，Y.Y. Li 和 C.-S. Lin 提出了一个公开问题：当 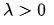 且 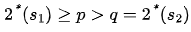 时，如下椭圆方程是否存在正解？(Arch. Ration. Mech. Anal. 203(3): 943-968, 2012)

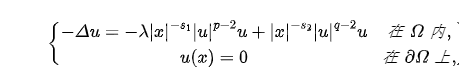
其中 是 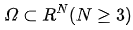为光滑有界区域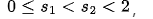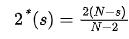， 为Hardy-Sobolev临界指数。

我们通过研究，首次对该问题部分情形给出否定性结论，同时得到存在性结果；并拓展研究了两类次临界情形与一类无界区域情形，获得正解存在性、分歧及非存在性等结论。

报告人简介： 唐之韵，博士，2025年博士研究生毕业于中南大学，自2025年8月至今于西南大学数学博士后流动站从事研究工作。主要研究方向为非线性泛函分析及其在偏微分方程中的应用。相关工作相继发表在Calc.Var and PDEs, J. Differential Equations, Commun. Anal. Mech., J. Appl. Anal. Comput. 等杂志。

Ground state solutions for the nonlinear Schrodinger-Bopp-

Podolsky system with potentials

李麟   重庆工商大学

报告摘要：In this paper, we consider the following nonlinear Schrodinger-Bopp-Podolsky system. By using some new analytic techniques and new inequalities, we prove the above system admits a ground state solution under mild assumptions on potential V and nonlinearity f. Moreover, we also give a simple minimax characterization of the ground state energy.

报告人简介：李麟，重庆工商大学足球投注网站 副教授，美国数学会特邀评论员。2015年西南大学获理学博士学位，导师为唐春雷教授和沈自飞教授。主要研究方向为临界点理论及其在微分方程中的应用。曾在University of California, Irvine访问，合作导师Martin Schechter教授。在《NA-TMA》、《NA-RWA》、《JMAA》、《TMNA》等杂志发表数篇论文。主持国家自然科学基金青年基金1项、重庆市科委自然科学基金1项、重庆市教委自然科学基金1项。

Multiplicity of normalized solutions for nonlinear Choquard equations

李贵东 贵州大学

报告摘要In this talk, we report our recent works about the existence of normalized solutions to Choquard equation. Under the general assumption of the nonlinear term F and within an appropriate mass range, we prove the existence and multiplicity of solutions to Choquard equation, which may manifest as global minimizer, local minimizer, or mountain pass-type solutions.

报告人简介：李贵东，博士，硕士研究生导师，贵州大学特聘教授，美国数学会《Math. Review》评论员。研究方向为非线性泛函分析及其在偏微分方程的应用，已在《J. Differential Equations》《Nonlinearity》《Nonlinear Anal.》等国际权威数学期刊发表 30 余篇论文，其中SCI一区论文 7 篇，二区论文 5 篇；目前主持国家青年基金等 3 项科研项目, 还担任《Adv. Nonlinear Anal.》《J. Math. Anal. Appl》《Complex Variables and Elliptic Equations》《Communications in Nonlinear Science and Numerical Simulation》《Appl. Math. Lett.》《Qual. Theory Dyn. Syst》等SCI期刊审稿人。